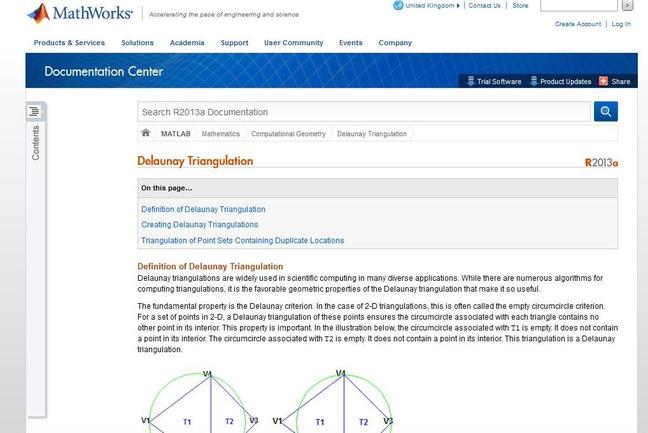
Delauny Trangulation Non-Uniform Mesh Generation
clf
clc
clear
N=30; % circle resolution as the number of points
hold on
% draw 1st circle at (0,0) radius 5 and get X and Y data
M=10
for i=1:M;
a=8*randn(1,1);
b=8*randn(1,1);
c=14;
plot(a,b,'ko')
H(i)=circle([a b],c,N);
end
grid on
xlabel('x')
ylabel('y')
hold on
axis equal
for i=1:M-1;
X1=get(H(i),'XData');
Y1=get(H(i),'YData');
X2=get(H(i+1),'XData');
Y2=get(H(i+1),'YData');
[x,y]=intersections(X1,Y1,X2,Y2,0)
x1(i)=x(1);
y1(i)=y(1);
x2(i)=x(2);
y2(i)=y(2);
plot(x,y,'ro')
end
hold on
for i=1:M-1;
f1=[ x2(i) x1(i)]
f2=[ y2(i) y1(i)]
f=line(f1,f2)
end
clc
clear
N=30; % circle resolution as the number of points
hold on
% draw 1st circle at (0,0) radius 5 and get X and Y data
M=10
for i=1:M;
a=8*randn(1,1);
b=8*randn(1,1);
c=14;
plot(a,b,'ko')
H(i)=circle([a b],c,N);
end
grid on
xlabel('x')
ylabel('y')
hold on
axis equal
for i=1:M-1;
X1=get(H(i),'XData');
Y1=get(H(i),'YData');
X2=get(H(i+1),'XData');
Y2=get(H(i+1),'YData');
[x,y]=intersections(X1,Y1,X2,Y2,0)
x1(i)=x(1);
y1(i)=y(1);
x2(i)=x(2);
y2(i)=y(2);
plot(x,y,'ro')
end
hold on
for i=1:M-1;
f1=[ x2(i) x1(i)]
f2=[ y2(i) y1(i)]
f=line(f1,f2)
end
Delaunay Trangulation Code for a Uniform Mesh
clf
clc
clear
N=30; % circle resolution as the number of points
hold on
% draw 1st circle at (0,0) radius 5 and get X and Y data
M=10
LX=12;
LY=12;
DX=LX/M;
DY=LY/M;
for i=1:M;
for j=1:M;
X(i,j)=i*DX;
Y(i,j)=j*DY;
a=X(i,j);
b=Y(i,j);
c=1;
plot(a,b,'ko')
H(i,j)=circle([a b],c,N);
end
end
grid on
xlabel('x')
ylabel('y')
hold on
axis equal
for i=1:M-1;
for j=1:M-1;
X1=get(H(i,j),'XData');
Y1=get(H(i,j),'YData');
X2=get(H(i+1,j+1),'XData');
Y2=get(H(i+1,j+1),'YData');
[x,y]=intersections(X1,Y1,X2,Y2,0)
x1(i)=x(1);
y1(i)=y(1);
x2(i)=x(2);
y2(i)=y(2);
plot(x,y,'ro')
end
end
hold on
for i=1:M-1;
f1=[ x2(i) x1(i)]
f2=[ y2(i) y1(i)]
f=line(f1,f2)
end
clc
clear
N=30; % circle resolution as the number of points
hold on
% draw 1st circle at (0,0) radius 5 and get X and Y data
M=10
LX=12;
LY=12;
DX=LX/M;
DY=LY/M;
for i=1:M;
for j=1:M;
X(i,j)=i*DX;
Y(i,j)=j*DY;
a=X(i,j);
b=Y(i,j);
c=1;
plot(a,b,'ko')
H(i,j)=circle([a b],c,N);
end
end
grid on
xlabel('x')
ylabel('y')
hold on
axis equal
for i=1:M-1;
for j=1:M-1;
X1=get(H(i,j),'XData');
Y1=get(H(i,j),'YData');
X2=get(H(i+1,j+1),'XData');
Y2=get(H(i+1,j+1),'YData');
[x,y]=intersections(X1,Y1,X2,Y2,0)
x1(i)=x(1);
y1(i)=y(1);
x2(i)=x(2);
y2(i)=y(2);
plot(x,y,'ro')
end
end
hold on
for i=1:M-1;
f1=[ x2(i) x1(i)]
f2=[ y2(i) y1(i)]
f=line(f1,f2)
end
Note :The interseactions code wasnt written by me
Note: The circle code wasnt written by me
function H=circle(center,radius,NOP,style)
%---------------------------------------------------------------------------------------------
% H=CIRCLE(CENTER,RADIUS,NOP,STYLE)
% This routine draws a circle with center defined as
% a vector CENTER, radius as a scaler RADIS. NOP is
% the number of points on the circle. As to STYLE,
% use it the same way as you use the rountine PLOT.
% Since the handle of the object is returned, you
% use routine SET to get the best result.
%
% Usage Examples,
%
% circle([1,3],3,1000,':');
% circle([2,4],2,1000,'--');
%
% Zhenhai Wang <zhenhai@ieee.org>
% Version 1.00
% December, 2002
%---------------------------------------------------------------------------------------------
if (nargin <3),
error('Please see help for INPUT DATA.');
elseif (nargin==3)
'b-';
end;
THETA=linspace(0,2*pi,NOP);
RHO=ones(1,NOP)*radius;
[X,Y] = pol2cart(THETA,RHO);
X=X+center(1);
Y=Y+center(2);
H=plot(X,Y,style);
axis square;
%---------------------------------------------------------------------------------------------
% H=CIRCLE(CENTER,RADIUS,NOP,STYLE)
% This routine draws a circle with center defined as
% a vector CENTER, radius as a scaler RADIS. NOP is
% the number of points on the circle. As to STYLE,
% use it the same way as you use the rountine PLOT.
% Since the handle of the object is returned, you
% use routine SET to get the best result.
%
% Usage Examples,
%
% circle([1,3],3,1000,':');
% circle([2,4],2,1000,'--');
%
% Zhenhai Wang <zhenhai@ieee.org>
% Version 1.00
% December, 2002
%---------------------------------------------------------------------------------------------
if (nargin <3),
error('Please see help for INPUT DATA.');
elseif (nargin==3)
'b-';
end;
THETA=linspace(0,2*pi,NOP);
RHO=ones(1,NOP)*radius;
[X,Y] = pol2cart(THETA,RHO);
X=X+center(1);
Y=Y+center(2);
H=plot(X,Y,style);
axis square;
Delaunay Trangulation Theory
The following link provides some theory for trangulation:
1-http://www.cgal.org/Manual/3.2/doc_html/cgal_manual/Triangulation_3/Chapter_main.html
2-http://www.ian-ko.com/resources/triangulated_irregular_network.htm
3-http://research.engineering.wustl.edu/~adina.stoica/extras/proj/undergrad_research/Delaunay%20Diagram%20Representations%20for%20Use%20in%20Image%20Near-Duplicate%20Detection.pdf
4-ftp://ip-62-245-106-89.net.upcbroadband.cz/books/Fem/bisectcr.pdf
5-http://www.weizmann.ac.il/matlab/techdoc/ref/delaunay.html
6-http://stackoverflow.com/questions/1700522/matlab-create-delaunay-triangulation-with-opening
7-http://people.sc.fsu.edu/~jburkardt/html/delaunay.html
1-http://www.cgal.org/Manual/3.2/doc_html/cgal_manual/Triangulation_3/Chapter_main.html
2-http://www.ian-ko.com/resources/triangulated_irregular_network.htm
3-http://research.engineering.wustl.edu/~adina.stoica/extras/proj/undergrad_research/Delaunay%20Diagram%20Representations%20for%20Use%20in%20Image%20Near-Duplicate%20Detection.pdf
4-ftp://ip-62-245-106-89.net.upcbroadband.cz/books/Fem/bisectcr.pdf
5-http://www.weizmann.ac.il/matlab/techdoc/ref/delaunay.html
6-http://stackoverflow.com/questions/1700522/matlab-create-delaunay-triangulation-with-opening
7-http://people.sc.fsu.edu/~jburkardt/html/delaunay.html
Delaunay Trangulation MATLAB
The following link is the best till now I found about delauny trangulation:
1-http://www.mathworks.co.uk/help/matlab/math/delaunay-triangulation.html
2-http://people.sc.fsu.edu/~jburkardt/m_src/triangulation/triangulation.html
3-http://www.s-hull.org/
4-http://www.mathworks.co.uk/help/matlab/math/triangulation-representations.html
5-http://www.unc.edu/~alfredo/pelosab/generate_mesh.m
1-http://www.mathworks.co.uk/help/matlab/math/delaunay-triangulation.html
2-http://people.sc.fsu.edu/~jburkardt/m_src/triangulation/triangulation.html
3-http://www.s-hull.org/
4-http://www.mathworks.co.uk/help/matlab/math/triangulation-representations.html
5-http://www.unc.edu/~alfredo/pelosab/generate_mesh.m
Delaunay Trangulation Algorthim
Under Construction. The following link is for :Delaunay Triangulation Algorithm and Application to Terrain Generation :
http://users-deprecated.aims.ac.za/~faniry/documents/faniry.pdf
http://users-deprecated.aims.ac.za/~faniry/documents/faniry.pdf
A ready Code written in matlab provided in function form : http://persson.berkeley.edu/distmesh/persson04mesh.pdf
The follwoing link also gives the option for the use of a Code : http://cran.r-project.org/web/packages/geometry/geometry.pdf
2-D Example
load seamount
plot(x,y,'.','markersize',12)
xlabel('Longitude'), ylabel('Latitude')
grid on
tri = delaunay(x,y);
hold on, triplot(tri,x,y), hold off
plot(x,y,'.','markersize',12)
xlabel('Longitude'), ylabel('Latitude')
grid on
tri = delaunay(x,y);
hold on, triplot(tri,x,y), hold off
Additional Infromation links:
1-http://image.diku.dk/kenny/download/vriphys10_course/meshing.pdf
2-http://www.google.co.uk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=13&ved=0CD4QFjACOAo&url=http%3A%2F%2Fwww2.warwick.ac.uk%2Ffac%2Fsci%2Fmoac%2Fpeople%2Fstudents%2F2010%2Fharold_moyse%2Fteaching%2Fmeshgenerationpresentation2.pptx&ei=5CKyUeCLLMO90QWp2YHwBw&usg=AFQjCNGPqLro_04SJGfKEx5ONcMIqxAGLg&sig2=Gm11BAqe-90WFzr8sl4hvw
3-http://graphics.stanford.edu/courses/cs368-06-spring/handouts/Delaunay_1.pdf
1-http://image.diku.dk/kenny/download/vriphys10_course/meshing.pdf
2-http://www.google.co.uk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=13&ved=0CD4QFjACOAo&url=http%3A%2F%2Fwww2.warwick.ac.uk%2Ffac%2Fsci%2Fmoac%2Fpeople%2Fstudents%2F2010%2Fharold_moyse%2Fteaching%2Fmeshgenerationpresentation2.pptx&ei=5CKyUeCLLMO90QWp2YHwBw&usg=AFQjCNGPqLro_04SJGfKEx5ONcMIqxAGLg&sig2=Gm11BAqe-90WFzr8sl4hvw
3-http://graphics.stanford.edu/courses/cs368-06-spring/handouts/Delaunay_1.pdf
3-D Example
figure
hidden on
trimesh(tri,x,y,z)
xlabel('Longitude'),ylabel('Latitude'),zlabel('Depth in Feet');
hidden on
trimesh(tri,x,y,z)
xlabel('Longitude'),ylabel('Latitude'),zlabel('Depth in Feet');
Mesh Refinment Methods
https://www.cs.cmu.edu/~quake/tripaper/triangle3.html