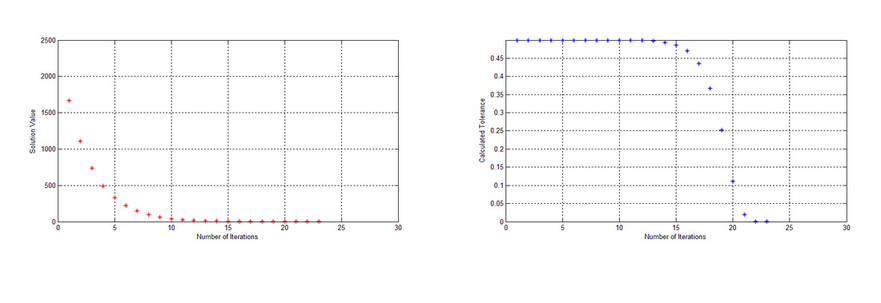
Newton Raphson Method

clc
clear
f = @(x) x^3-2*x;            
fprime = @(x) 3*x^2-2 ;         
tolerancetarget = 10^(-7);        
epsilon = 10^(-16);          
 
maxIterations = 30;               
have_We_Found_Solution = false;       
 x0(1) = 2500;
for i = 1:maxIterations; 
    y(i) = f(x0(i));
    yprime(i) = fprime(x0(i));
 
    if(abs(yprime(i)) < epsilon)                                
        fprintf('WARNING: denominator is too small\n')
        break;                                                 
    end
 
    x1(i)= x0(i)-y(i)/yprime(i);                                % Newton Raphson computation
    
    calculatedtolerance(i)=abs(x1(i)- x0(i))/abs(x1(i));
 
    if(calculatedtolerance(i) < tolerancetarget)             
        have_We_Found_Solution = true
        break;                                                %Done
    end
 x0(i+1) = x1(i);
 pause(1)
 
 h1(i) = subplot(221);
 set(h1(i),'XLim',[0 maxIterations],'YLim',[0 x0(1)])
 plot(i,x1(i),'r-*')
grid on
xlabel('Number of Iterations')
ylabel('Solution Value')
hold on

h2(i) = subplot(222);
set(h2(i),'XLim',[0 maxIterations],'YLim',[0 calculatedtolerance(1)])
plot(i,calculatedtolerance(i),'b-*')
grid on
xlabel('Number of Iterations')
ylabel(' Calculated Tolerance')
hold on
end
 if (have_We_Found_Solution) % We found a solution within tolerance and maximum number of iterations
    fprintf('The root is: %f\n', x1);
else %If we weren't able to find a solution to within the desired tolerance
    fprintf('Warning: Not able to find solution to within the desired tolerance of %f\n', tolerance);
    fprintf('The last computed approximate root was %f\n', x1)
 end

set(1, 'units', 'centimeters', 'pos', [0 0 120.5 100])

---

Unless otherwise noted, all content on this site is @Copyright by Ahmed Al Makky 2012-2014 - http://cfd2012.com