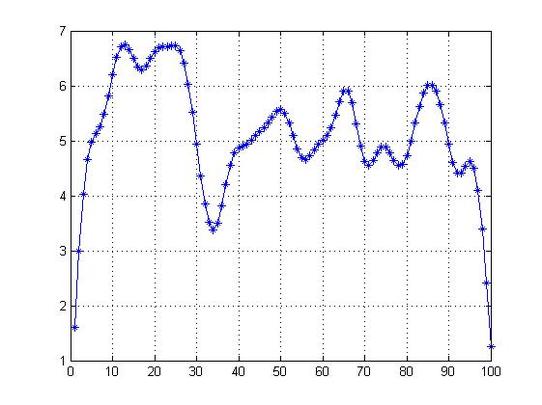
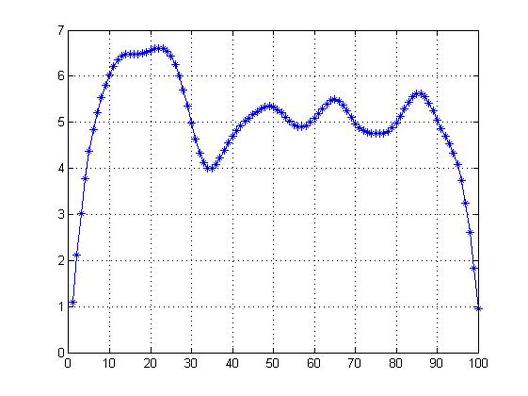
Flow Diffusion using Crank Nicholsion

clc
clear
M=100;
N=10;
LX=1;
LY=1;
TIME0=0;
TIME=1;
tt=1000;
Dt=(TIME-TIME0)/tt;
D=12e-4;
DX=LX/M;
DY=LY/N;
mu=D*Dt/(DX)^2;
%Initilization Matrix
for t=1:1;
    for i=2:M-1;
            U(i,t)=10*rand(1,1);
    end
end
%Boundary Conditions
for t=1:1;
U(1,t)=0;
U(M,t)=0;
end

for t=1:1;
    for i=1:1;
            d(i,t)=mu*U(i+1,t)+(1-2*mu)*U(i,t);
    end
end

for t=1:1;
    for i=2:M-1;
            d(i,t)=mu*U(i+1,t)+(1-2*mu)*U(i,t)+mu*U(i-1,t);
    end
end

for t=1:1;
    for i=M:M;
            d(i,t)=(1-2*mu)*U(i,t)+mu*U(i-1,t);
    end
end

%Constructing the Diagonal Matrix
a=ones(M-1,1)
b=ones(M,1)
g=(1+2*mu)*diag(b)-mu*diag(a,-1)-mu*diag(a,1)
gg=g^-1

for t=1:1;
U(:,t)=gg*d(:,t)
end

for t=1:tt;
    for i=1:1;
            d(i,t)=mu*U(i+1,t)+(1-2*mu)*U(i,t);
    end
    for i=2:M-1;
            d(i,t)=mu*U(i+1,t)+(1-2*mu)*U(i,t)+mu*U(i-1,t);
    end
    for i=M:M;
            d(i,t)=(1-2*mu)*U(i,t)+mu*U(i-1,t);
    end
U(:,t+1)=gg*d(:,t)
end

for t=1:tt;
plot(U(:,t),'-*')
grid on
pause(0.4)
close
end

With the progression of time the flow should turn to be more parabolic.

---

Unless otherwise noted, all content on this site is @Copyright by Ahmed Al Makky 2012-2013 - http://cfd2012.com