Constructing a Diagonal Matrix Problem
clc
clear
N=10;
k=1;
A=1;
dx=0.01;
b=[1:1:N+1];
for i=1:N;
aw(i)=(k*A)/dx;
ae(i)=(k*A)/dx;
ap(i)=aw(i)+ae(i);
b(i)=randn(1,1);
end
ap(11)=0;
ae(10)=0;
aw(10)=0;
Tp=diag(ap,0);
Tw=diag(aw,-1);
Te=diag(ae,1);
Tw;
Tp;
Te;
un=Tw+Te+Tp
unn=(un)^-1
T=b*unn
%This Code generates a set of data then calculates the traveled distance in
%xy plane and finaly sets up a diagonal matrix that finds the required unknowns
clc
clear
N=6;
% This section generates two one dimensional data matricies.
for i=1:2*N;
x(i)=randn(1,1);
y(i)=randn(1,1);
end
% This section subtracts the data from two one dimensional matrcies
% and stores them in a new matrix .
for i=1:10;
z(i)=x(i)-y(i);
end
% This section assignes the generated data to the diagonal part of the matrix
%initilization paramters:
i=0;
a=0;
b=0;
k=1;
for j=1:N;
i=i+1;
deltax(j)=x(i+1)-x(i);
deltay(j)=y(i+1)-y(i);
s = [deltax(j) deltay(j)];
%Finding the traveled distance for a each studied point
distance(j)=norm(s);
a=a+1;
b=b+1;
c=deltax(j);
pp=[ c ]
ss(a,b)=pp
end
% This gives the value of the traveld distance of the random generated data
r=sum(distance(:))
% This section assignes the generated data to the upper diagonal part of the matrix
%initilization paramters:
a=1;
k=0;
i=0;
for j=1:N-1;
i=i+1;
deltax(j)=x(i+1)-x(i);
deltay(j)=y(i+1)-y(i);
a=a+1;
k=k+1;
ss1(a,k)=deltax(j);
end
%This adds a cell to the generated matrix to have the same dimension as the
%diagonal matrix
ss1(a,k+1)=0;
% This section assignes the generated data to the lower diagonal part of the matrix
%initilization paramters:
b=1;
k=0;
i=0;
for j=1:N-1;
i=i+1;
deltax(j)=x(i+1)-x(i);
deltay(j)=y(i+1)-y(i);
b=b+1;
k=k+1;
ss2(k,b)=deltay(j);
end
%This adds a cell to the generated matrix to have the same dimension as the
%diagonal matrix
ss2(k+1,b)=0;
% This section adds up the three diagonal parts of
% the matrix
sst=ss1+ss2+ss
% This section generates one dimensional data matriX.
for i=1:N;
d(i)=randn(1,1);
end
% Finding the unknown values of the several formulated equations
u=d/(sst)
clear
N=10;
k=1;
A=1;
dx=0.01;
b=[1:1:N+1];
for i=1:N;
aw(i)=(k*A)/dx;
ae(i)=(k*A)/dx;
ap(i)=aw(i)+ae(i);
b(i)=randn(1,1);
end
ap(11)=0;
ae(10)=0;
aw(10)=0;
Tp=diag(ap,0);
Tw=diag(aw,-1);
Te=diag(ae,1);
Tw;
Tp;
Te;
un=Tw+Te+Tp
unn=(un)^-1
T=b*unn
%This Code generates a set of data then calculates the traveled distance in
%xy plane and finaly sets up a diagonal matrix that finds the required unknowns
clc
clear
N=6;
% This section generates two one dimensional data matricies.
for i=1:2*N;
x(i)=randn(1,1);
y(i)=randn(1,1);
end
% This section subtracts the data from two one dimensional matrcies
% and stores them in a new matrix .
for i=1:10;
z(i)=x(i)-y(i);
end
% This section assignes the generated data to the diagonal part of the matrix
%initilization paramters:
i=0;
a=0;
b=0;
k=1;
for j=1:N;
i=i+1;
deltax(j)=x(i+1)-x(i);
deltay(j)=y(i+1)-y(i);
s = [deltax(j) deltay(j)];
%Finding the traveled distance for a each studied point
distance(j)=norm(s);
a=a+1;
b=b+1;
c=deltax(j);
pp=[ c ]
ss(a,b)=pp
end
% This gives the value of the traveld distance of the random generated data
r=sum(distance(:))
% This section assignes the generated data to the upper diagonal part of the matrix
%initilization paramters:
a=1;
k=0;
i=0;
for j=1:N-1;
i=i+1;
deltax(j)=x(i+1)-x(i);
deltay(j)=y(i+1)-y(i);
a=a+1;
k=k+1;
ss1(a,k)=deltax(j);
end
%This adds a cell to the generated matrix to have the same dimension as the
%diagonal matrix
ss1(a,k+1)=0;
% This section assignes the generated data to the lower diagonal part of the matrix
%initilization paramters:
b=1;
k=0;
i=0;
for j=1:N-1;
i=i+1;
deltax(j)=x(i+1)-x(i);
deltay(j)=y(i+1)-y(i);
b=b+1;
k=k+1;
ss2(k,b)=deltay(j);
end
%This adds a cell to the generated matrix to have the same dimension as the
%diagonal matrix
ss2(k+1,b)=0;
% This section adds up the three diagonal parts of
% the matrix
sst=ss1+ss2+ss
% This section generates one dimensional data matriX.
for i=1:N;
d(i)=randn(1,1);
end
% Finding the unknown values of the several formulated equations
u=d/(sst)
Successive Over Relaxation Code
clc
clear
it=100
A=[2 1; 5 7]
b=[11 13]
x(1:2,1)=[100 100]
D = diag(A,0)
D_1=[1/D(1,1) 0; 0 1/D(2,1)]
L=tril(A,-1)
U=triu(A,+1)
T=D_1*(-L-U)
C=D_1*b.'
x(1:2,2)=T*x+C;
x(1:2,2)
for i=1:it;
x(1:2,i+1)=T*x(1:2,i)+C
end
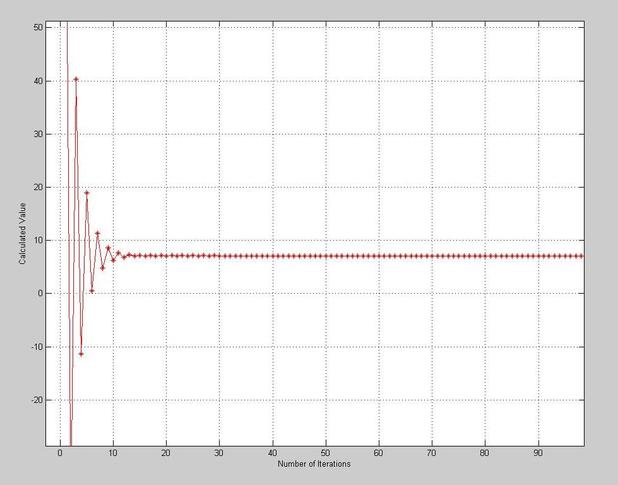
figure(1)
for i=1:it;
plot(x(1,1:i),'r-*')
hold on
end
axis equal
xlabel('Number of Iterations')
ylabel('Calculated Value')
grid on
hold off
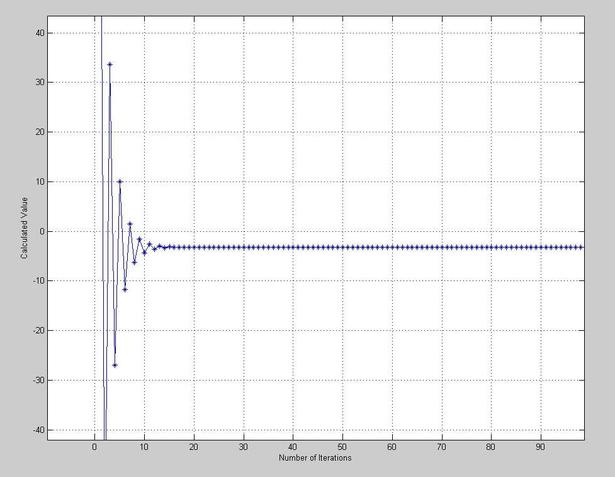
figure(2)
for i=1:it;
plot(x(2,1:i),'b-*')
hold on
end
axis equal
xlabel('Number of Iterations')
ylabel('Calculated Value')
grid on
clear
it=100
A=[2 1; 5 7]
b=[11 13]
x(1:2,1)=[100 100]
D = diag(A,0)
D_1=[1/D(1,1) 0; 0 1/D(2,1)]
L=tril(A,-1)
U=triu(A,+1)
T=D_1*(-L-U)
C=D_1*b.'
x(1:2,2)=T*x+C;
x(1:2,2)
for i=1:it;
x(1:2,i+1)=T*x(1:2,i)+C
end
figure(1)
for i=1:it;
plot(x(1,1:i),'r-*')
hold on
end
axis equal
xlabel('Number of Iterations')
ylabel('Calculated Value')
grid on
hold off
figure(2)
for i=1:it;
plot(x(2,1:i),'b-*')
hold on
end
axis equal
xlabel('Number of Iterations')
ylabel('Calculated Value')
grid on
Additional Links
http://www.mathworks.co.uk/help/matlab/ref/tril.html
http://www.mathworks.co.uk/help/matlab/ref/diag.html
http://www.mathworks.co.uk/help/matlab/ref/triu.html
http://www.mathworks.co.uk/matlabcentral/fileexchange/28226-successive-over-relaxation/content/sor.m
Unless otherwise noted, all content on this site is @Copyright by Ahmed Al Makky 2012-2013 - http://cfd2012.com