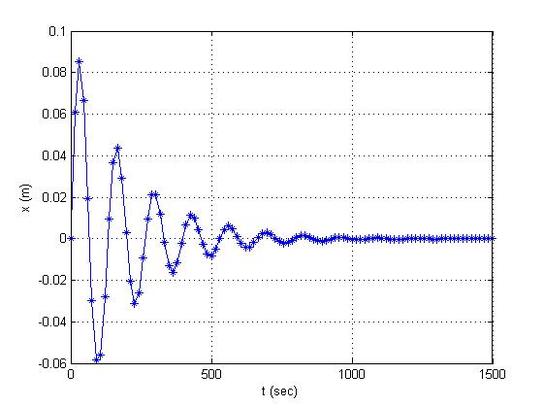
Free Vibration with Damping Modelling
The following code was written based on the theory provided in the following link: http://en.wikipedia.org/wiki/Vibration
clc
clear
C=1e-4;
Cc=10e-4;
K=1;
ksi=C/Cc
m=0.01;
Cc=2*m*(K/m)^0.5;
wn=(K/m)^0.5;
eqn2= 'm*D2x+C*Dx+K*x=0';
init2= 'x(0)=0,Dx(0)=1';
x=dsolve(eqn2,init2,'t')
t=linspace(0,1500,100);
z=eval(vectorize(x));
plot(t,z,'-*')
xlabel('t (sec)')
ylabel('x (m)')
grid on
clear
C=1e-4;
Cc=10e-4;
K=1;
ksi=C/Cc
m=0.01;
Cc=2*m*(K/m)^0.5;
wn=(K/m)^0.5;
eqn2= 'm*D2x+C*Dx+K*x=0';
init2= 'x(0)=0,Dx(0)=1';
x=dsolve(eqn2,init2,'t')
t=linspace(0,1500,100);
z=eval(vectorize(x));
plot(t,z,'-*')
xlabel('t (sec)')
ylabel('x (m)')
grid on
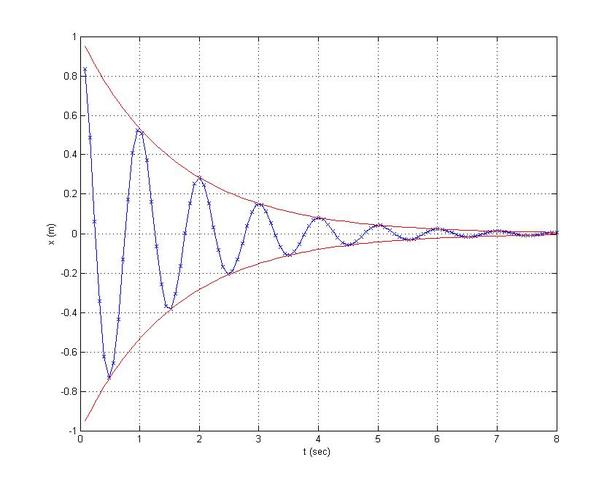
Damped and Undamped Natural Frequencies
The following code was written based on the theory provided in the following link: http://en.wikipedia.org/wiki/Vibration
clc
clear
x0=1;
c=2e-5;
k=1e-6;
m=0.01;
cc=2*(k*m)^0.5;
ksi=c/cc;
t0=0;
tt=8;
M=100
dt=(tt-t0)/M;
fn=1;
wn=2*pi*fn;
fi=0;
for i=1:M;
t(i)=i*dt;
b=(1-ksi^2)^0.5;
xx(i)=x0*exp(-ksi*wn*t(i));
xxx(i)=-x0*exp(-ksi*wn*t(i));
x(i)=xx(i)*cos(b*wn*t(i)-fi);
end
plot(t,x,'-x')
xlabel('t (sec)')
ylabel('x (m)')
grid on
hold on
plot(t,xx,'r-')
hold on
plot(t,xxx,'r-')
clear
x0=1;
c=2e-5;
k=1e-6;
m=0.01;
cc=2*(k*m)^0.5;
ksi=c/cc;
t0=0;
tt=8;
M=100
dt=(tt-t0)/M;
fn=1;
wn=2*pi*fn;
fi=0;
for i=1:M;
t(i)=i*dt;
b=(1-ksi^2)^0.5;
xx(i)=x0*exp(-ksi*wn*t(i));
xxx(i)=-x0*exp(-ksi*wn*t(i));
x(i)=xx(i)*cos(b*wn*t(i)-fi);
end
plot(t,x,'-x')
xlabel('t (sec)')
ylabel('x (m)')
grid on
hold on
plot(t,xx,'r-')
hold on
plot(t,xxx,'r-')
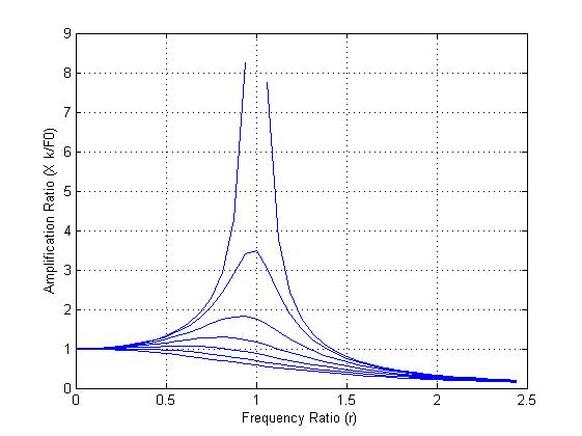
Forced Vibration with Camping
The following code was written based on the theory provided in the following link: http://en.wikipedia.org/wiki/Vibration
clc
clear
M=40;
fn=2;
F0=1;
K=1e3;
ksi0=0;
ksi00=1;
N=7;
dksi=(ksi00-ksi0)/N;
ksi(1:M,1)=0;
for j=1:N;
ksi(1:M,j+1)=ksi(1:M,j)+dksi;
end
f0=0;
ff0=5;
df=(ff0-f0)/M;
f(1,1:M)=0;
for i=1:M;
f(i+1,1:N)=f(i,1:N)+df;
end
for j=1:N;
for i=1:M;
r(i,j)=f(i,j)/fn;
fii(i,j)=atan((2*ksi(i,j)*r(i,j)/(1-r(i,j)^2)));
fi(i,j)=(180/pi)*fii(i,j);
bb(i,j)=(1-r(i,j)^2)^2+(2*ksi(i,j)*r(i,j))^2;
bbb(i,j)=1/bb(i,j)^0.5;
x0(i,j)=(F0/K)*bbb(i,j);
xx0(i,j)=(K/F0)*x0(i,j);
end
end
for j=1:N;
plot(r(:,j),xx0(:,j),'-')
hold on
end
xlabel('Frequency Ratio (r)')
ylabel('Amplification Ratio (X k/F0)')
grid on
hold off
figure(2)
for j=1:N;
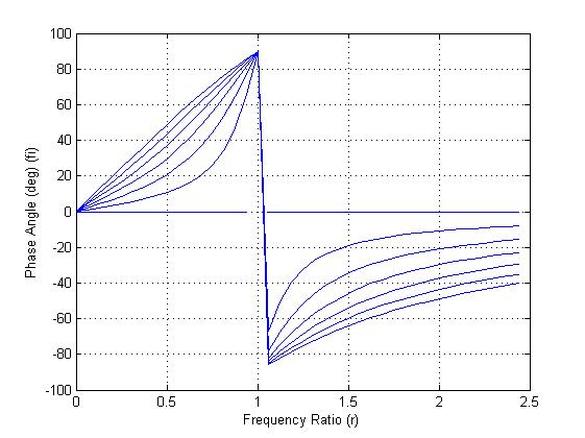
plot(r(1:M,j),fi(1:M,j),'-')
hold on
end
xlabel('Frequency Ratio (r)')
ylabel('Phase Angle (deg) (fi)')
grid on
clear
M=40;
fn=2;
F0=1;
K=1e3;
ksi0=0;
ksi00=1;
N=7;
dksi=(ksi00-ksi0)/N;
ksi(1:M,1)=0;
for j=1:N;
ksi(1:M,j+1)=ksi(1:M,j)+dksi;
end
f0=0;
ff0=5;
df=(ff0-f0)/M;
f(1,1:M)=0;
for i=1:M;
f(i+1,1:N)=f(i,1:N)+df;
end
for j=1:N;
for i=1:M;
r(i,j)=f(i,j)/fn;
fii(i,j)=atan((2*ksi(i,j)*r(i,j)/(1-r(i,j)^2)));
fi(i,j)=(180/pi)*fii(i,j);
bb(i,j)=(1-r(i,j)^2)^2+(2*ksi(i,j)*r(i,j))^2;
bbb(i,j)=1/bb(i,j)^0.5;
x0(i,j)=(F0/K)*bbb(i,j);
xx0(i,j)=(K/F0)*x0(i,j);
end
end
for j=1:N;
plot(r(:,j),xx0(:,j),'-')
hold on
end
xlabel('Frequency Ratio (r)')
ylabel('Amplification Ratio (X k/F0)')
grid on
hold off
figure(2)
for j=1:N;
plot(r(1:M,j),fi(1:M,j),'-')
hold on
end
xlabel('Frequency Ratio (r)')
ylabel('Phase Angle (deg) (fi)')
grid on
The second plot didn't mimic the original one because after Angle 90 deg there should be addition to 180 instead of the negative values.
Unless otherwise noted, all content on this site is @Copyright by Ahmed Al Makky 2012-2013 - http://cfd2012.com