Second Order Derivate
clc
clear
LX=1;
N=100;
dx=LX/N;
for i=1:N+2;
x(i)=i*dx
u(i)=0.1*rand(1,1)%exp(-x(i))
v(i)=(x(i))^2+(x(i))
end
for i=1:N;
j=j+1
dudx(i)=(u(i+1)-u(i))/dx
dvdx(i)=(v(i+1)-v(i))/dx
end
for i=2:N+1;
duudx(i)=(u(i+1)-u(i-1))/(2*dx)
end
plot(u,'r')
hold on
plot(duudx,'r')
plot(dudx)
axis equal
grid on
figure(2)
plot(dvdx)
axis equal
grid on
pause(10)
close all
clear
LX=1;
N=100;
dx=LX/N;
for i=1:N+2;
x(i)=i*dx
u(i)=0.1*rand(1,1)%exp(-x(i))
v(i)=(x(i))^2+(x(i))
end
for i=1:N;
j=j+1
dudx(i)=(u(i+1)-u(i))/dx
dvdx(i)=(v(i+1)-v(i))/dx
end
for i=2:N+1;
duudx(i)=(u(i+1)-u(i-1))/(2*dx)
end
plot(u,'r')
hold on
plot(duudx,'r')
plot(dudx)
axis equal
grid on
figure(2)
plot(dvdx)
axis equal
grid on
pause(10)
close all
Derivative of Seven Given Points
clc
clear
x=[1:0.2:2.2];
y=[ 2.7183 3.3201 4.0552 4.9530 6.0496 7.3891 9.0250 ];
N=size(x);
M=size(y);
NN=max(N);
MM=max(M);
j=0;
for i=1:MM-1;
j=j+1;
y1(j)=y(i+1)-y(i);
%pause
%y1
end
MMM=size(y1);
MMMM=max(MMM)
j=0;
for i=1:MMMM-1;
j=j+1;
y2(j)=y1(i+1)-y1(i);
%pause
%y2
end
MMMMM=size(y2);
MMMMMM=max(MMMMM)
j=0;
for i=1:MMMMMM-1;
j=j+1;
y3(j)=y2(i+1)-y2(i);
%pause
%y3
end
b=size(y3);
bb=max(b)
j=0;
for i=1:bb-1;
j=j+1;
y4(j)=y3(i+1)-y3(i);
%pause
%y4
end
bbb=size(y4);
bbbb=max(bbb)
j=0;
for i=1:bbbb-1;
j=j+1;
y5(j)=y4(i+1)-y4(i);
%pause
%y5
end
c=size(y5);
f=size(y5);
ff=max(f)
j=0;
for i=1:ff-1;
j=j+1;
y6(j)=y5(i+1)-y5(i);
%pause
%y6
end
f=size(y6);
ff=max(f)
u1= [ y(1) y1(1) y2(1) y3(1) y4(1) y5(1) y6(1) ]
u2= [ y(2) y1(2) y2(2) y3(2) y4(2) y5(2) ]
u3= [ y(3) y1(3) y2(3) y3(3) y4(3)]
u4= [ y(4) y1(4) y2(4) y3(4)]
u5= [ y(5) y1(5) y2(5)]
u6= [ y(6) y1(6) ]
u7= [ y(7) ]
y'
y1'
y2'
y3'
y4'
y5'
y6'
h=0.2;
dydx=(1/h)*(y1(2)-0.5*y2(2)+(1/3)*y3(2)-0.25* y4(2)+(1/5)*y5(2))
clear
x=[1:0.2:2.2];
y=[ 2.7183 3.3201 4.0552 4.9530 6.0496 7.3891 9.0250 ];
N=size(x);
M=size(y);
NN=max(N);
MM=max(M);
j=0;
for i=1:MM-1;
j=j+1;
y1(j)=y(i+1)-y(i);
%pause
%y1
end
MMM=size(y1);
MMMM=max(MMM)
j=0;
for i=1:MMMM-1;
j=j+1;
y2(j)=y1(i+1)-y1(i);
%pause
%y2
end
MMMMM=size(y2);
MMMMMM=max(MMMMM)
j=0;
for i=1:MMMMMM-1;
j=j+1;
y3(j)=y2(i+1)-y2(i);
%pause
%y3
end
b=size(y3);
bb=max(b)
j=0;
for i=1:bb-1;
j=j+1;
y4(j)=y3(i+1)-y3(i);
%pause
%y4
end
bbb=size(y4);
bbbb=max(bbb)
j=0;
for i=1:bbbb-1;
j=j+1;
y5(j)=y4(i+1)-y4(i);
%pause
%y5
end
c=size(y5);
f=size(y5);
ff=max(f)
j=0;
for i=1:ff-1;
j=j+1;
y6(j)=y5(i+1)-y5(i);
%pause
%y6
end
f=size(y6);
ff=max(f)
u1= [ y(1) y1(1) y2(1) y3(1) y4(1) y5(1) y6(1) ]
u2= [ y(2) y1(2) y2(2) y3(2) y4(2) y5(2) ]
u3= [ y(3) y1(3) y2(3) y3(3) y4(3)]
u4= [ y(4) y1(4) y2(4) y3(4)]
u5= [ y(5) y1(5) y2(5)]
u6= [ y(6) y1(6) ]
u7= [ y(7) ]
y'
y1'
y2'
y3'
y4'
y5'
y6'
h=0.2;
dydx=(1/h)*(y1(2)-0.5*y2(2)+(1/3)*y3(2)-0.25* y4(2)+(1/5)*y5(2))
Plane Derivative Mapping
clc
clear
LX=1;
LY=1;
N=4;
M=4;
dx=LX/M
dy=LY/N
for t=1:3
for i=1:M;
for j=1:N;
x(i,j,t)=(i)*dx-dx
x(i+1,j,t)=i*dx
x(i+2,j,t)=i*dx+dx
u(i+2,j,t)=(x(i+2,j,t))^2
u(i+1,j,t)=(x(i+1,j,t))^2
u(i,j,t)=(x(i,j,t))^2
d2udx2(i,j,t)=(u(i+2,j,t)-2*u(i+1,j,t)+u(i,j,t))/(dx)^2
end
end
end
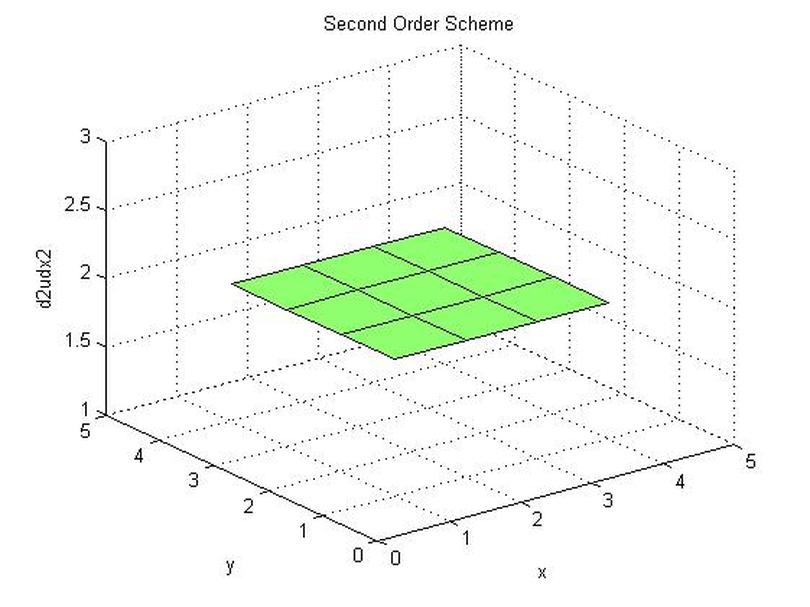
surf(d2udx2(:,:,2))
set(gca,'XLim',[0 5],'YLim',[0 5])
title('Second Order Scheme')
xlabel('x')
ylabel('y')
zlabel('d2udx2')
clear
LX=1;
LY=1;
N=4;
M=4;
dx=LX/M
dy=LY/N
for t=1:3
for i=1:M;
for j=1:N;
x(i,j,t)=(i)*dx-dx
x(i+1,j,t)=i*dx
x(i+2,j,t)=i*dx+dx
u(i+2,j,t)=(x(i+2,j,t))^2
u(i+1,j,t)=(x(i+1,j,t))^2
u(i,j,t)=(x(i,j,t))^2
d2udx2(i,j,t)=(u(i+2,j,t)-2*u(i+1,j,t)+u(i,j,t))/(dx)^2
end
end
end
surf(d2udx2(:,:,2))
set(gca,'XLim',[0 5],'YLim',[0 5])
title('Second Order Scheme')
xlabel('x')
ylabel('y')
zlabel('d2udx2')
Unless otherwise noted, all content on this site is @Copyright by Ahmed Al Makky 2012-2013 - http://cfd2012.com