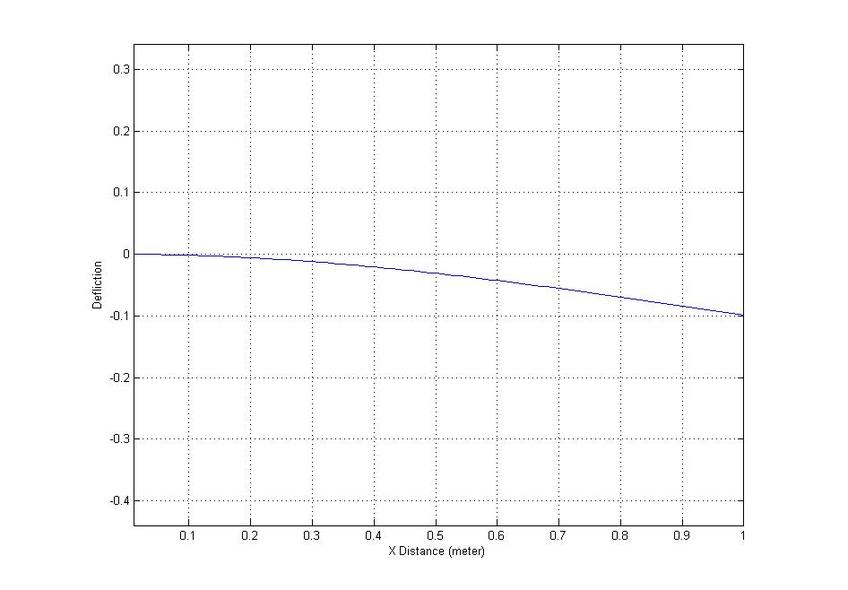
Cantilever Beam Analysis
This an initial trial for one that dosnt change with time, I aim to add a time changing one later.
clc
clear
E=69e12;
D=0.005;
A=0.25*(pi)*(D)^2;
I=(pi/4)*(D)^4;
L=1;
P=-10000;
PP=(P/(6*E*I));
M=100;
DX=L/M;
for i=1:M;
X(i)=i*DX;
Y(i)=PP*((X(i))^2)*(3*L-X(i))
end
plot(X,Y)
grid on
xlabel('X Distance (meter)')
ylabel('Defliction')
axis equal
clear
E=69e12;
D=0.005;
A=0.25*(pi)*(D)^2;
I=(pi/4)*(D)^4;
L=1;
P=-10000;
PP=(P/(6*E*I));
M=100;
DX=L/M;
for i=1:M;
X(i)=i*DX;
Y(i)=PP*((X(i))^2)*(3*L-X(i))
end
plot(X,Y)
grid on
xlabel('X Distance (meter)')
ylabel('Defliction')
axis equal
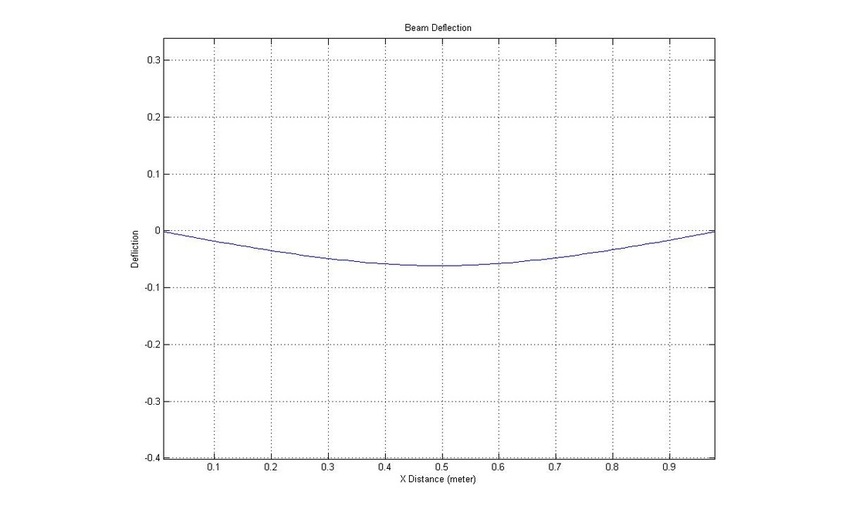
Beam Deflection (Symetrical Beam)
The force is acting on the midsection of the beam
clc
clear
E=69e12;
D=0.005;
A=0.25*(pi)*(D)^2;
I=(pi/4)*(D)^4;
L=1;
P=-100000;
PP=(P/(12*E*I));
PPP=3/4
M=100;
DX=L/M;
for i=1:M/2;
X(i)=i*DX;
Y(i)=PP*X(i)*(PPP*(L^2)-(X(i))^2)
end
ii=M/2
for i=M/2:M-2;
ii=ii-1
X(i)=i*DX;
Y(i)=Y(ii)
end
plot(X,Y)
grid on
xlabel('X Distance (meter)')
ylabel('Defliction')
title('Beam Deflection')
axis equal
clear
E=69e12;
D=0.005;
A=0.25*(pi)*(D)^2;
I=(pi/4)*(D)^4;
L=1;
P=-100000;
PP=(P/(12*E*I));
PPP=3/4
M=100;
DX=L/M;
for i=1:M/2;
X(i)=i*DX;
Y(i)=PP*X(i)*(PPP*(L^2)-(X(i))^2)
end
ii=M/2
for i=M/2:M-2;
ii=ii-1
X(i)=i*DX;
Y(i)=Y(ii)
end
plot(X,Y)
grid on
xlabel('X Distance (meter)')
ylabel('Defliction')
title('Beam Deflection')
axis equal
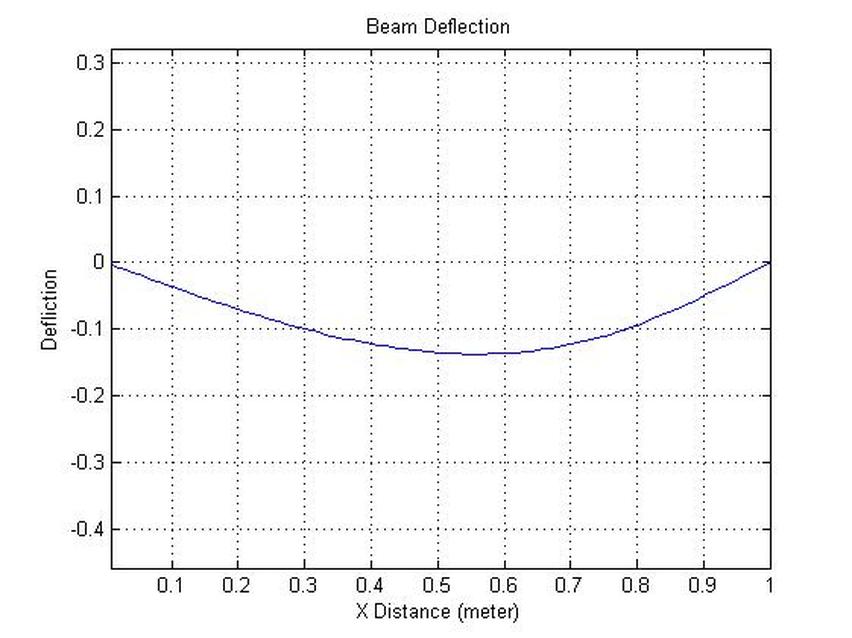
None Symetrical Beam Deflection
The acting force on th beam is not in the mid section.
clc
clear
E=69e12;
D=0.005;
A=0.25*(pi)*(D)^2;
I=(pi/4)*(D)^4;
L=1;
a=0.75;
b=0.25;
P=-320000;
PP=(P/(6*E*I*L));
PPP=3/4
M=100;
DX=L/M;
for i=1:a*M;
X(i)=i*DX;
Y(i)=PP*b*X(i)*((L^2)-(X(i))^2-(b)^2)
end
for i=a*M:M;
X(i)=i*DX;
Y(i)=PP*b*((L/b)*(X(i)-a)^3+(L^2-b^2)*X(i)-X(i)^3)
end
plot(X,Y)
grid on
xlabel('X Distance (meter)')
ylabel('Defliction')
title('Beam Deflection')
axis equal
clear
E=69e12;
D=0.005;
A=0.25*(pi)*(D)^2;
I=(pi/4)*(D)^4;
L=1;
a=0.75;
b=0.25;
P=-320000;
PP=(P/(6*E*I*L));
PPP=3/4
M=100;
DX=L/M;
for i=1:a*M;
X(i)=i*DX;
Y(i)=PP*b*X(i)*((L^2)-(X(i))^2-(b)^2)
end
for i=a*M:M;
X(i)=i*DX;
Y(i)=PP*b*((L/b)*(X(i)-a)^3+(L^2-b^2)*X(i)-X(i)^3)
end
plot(X,Y)
grid on
xlabel('X Distance (meter)')
ylabel('Defliction')
title('Beam Deflection')
axis equal
To write a code you will need the following links
1-http://en.wikipedia.org/wiki/Deflection_%28engineering%29
2-http://en.wikipedia.org/wiki/List_of_moment_of_areas
3-http://en.wikipedia.org/wiki/Bending
1-http://en.wikipedia.org/wiki/Deflection_%28engineering%29
2-http://en.wikipedia.org/wiki/List_of_moment_of_areas
3-http://en.wikipedia.org/wiki/Bending
The following provided link has all the dervied equations for alll the different beam configurations
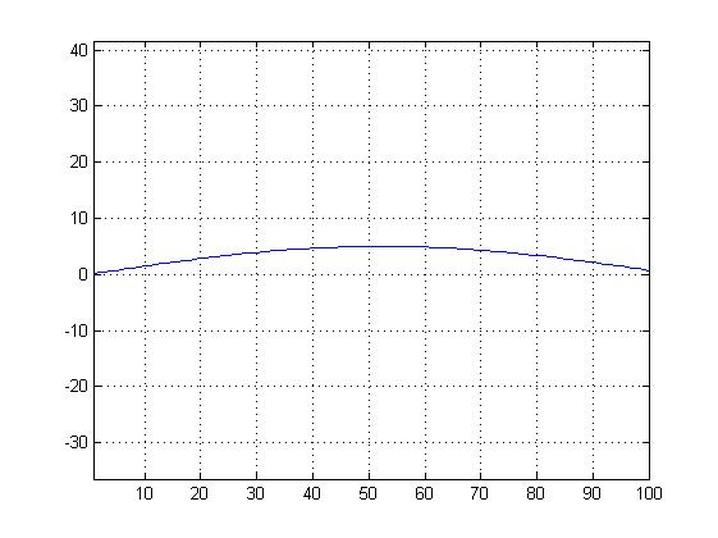
Example
clc
clear
M=100;
N=100;
x0=0;
x00=12;
dx=(x00-x0)/M;
t0=0;
t00=3;
dt=(t00-t0)/N;
E=1;
MU=1;
alpha1=(E/MU);
aplha2=(dt/dx);
alpha=(alpha1*aplha2)^2;
for i=1:M;
for t=1:3;
x(i)=i*dx;
y(i,t)=5*sin(0.25*x(i));
end
end
plot(1:1:M,y(1:1:M,1))
grid on
axis equal
%Left Handside
for t=2:N;
for i=2:M-2;
y(i,t+1)=alpha*(y(i+1,t)+y(i-1,t))+2*y(i,t)*(1-alpha)-y(i,t-1);
end
end
%Right Handside
for t=2:N;
for i=2:M-2;
y(i,t+1)=alpha*(y(i+1,t))+2*y(i,t)*(1-alpha)-y(i,t-1);
end
end
clear
M=100;
N=100;
x0=0;
x00=12;
dx=(x00-x0)/M;
t0=0;
t00=3;
dt=(t00-t0)/N;
E=1;
MU=1;
alpha1=(E/MU);
aplha2=(dt/dx);
alpha=(alpha1*aplha2)^2;
for i=1:M;
for t=1:3;
x(i)=i*dx;
y(i,t)=5*sin(0.25*x(i));
end
end
plot(1:1:M,y(1:1:M,1))
grid on
axis equal
%Left Handside
for t=2:N;
for i=2:M-2;
y(i,t+1)=alpha*(y(i+1,t)+y(i-1,t))+2*y(i,t)*(1-alpha)-y(i,t-1);
end
end
%Right Handside
for t=2:N;
for i=2:M-2;
y(i,t+1)=alpha*(y(i+1,t))+2*y(i,t)*(1-alpha)-y(i,t-1);
end
end
MATLAB Moment of Inertia
Code needs to be debuged not finished yet.
clc
clear
LX=1;
LY=1;
M=10;
N=10;
DX=LX/M;
DY=LY/N;
X0=0;
Y0=0;
ii=-1;
for i=1:M+1;
ii=ii+1;
jj=-1;
for j=1:N+1;
jj=jj+1;
X(i,j)=ii*DX+X0;
Y(i,j)=jj*DY+Y0;
DA(i,j)=(DX)*(DY);
end
end
a1=size(X)
a2=size(Y)
xc=sum(sum(X))/(a1(1)*a1(2))
yc=sum(sum(Y))/(a2(1)*a2(2))
for i=1:M+1;
for j=1:N+1;
IX(i,j)=((Y(i,j)-yc)^2)*DA(i,j);
end
end
ix=(1/12)*(LX)*(LY)^3
A=sum(sum(DA))
IXX=sum(sum(IX))/(a1(1)*a1(2))
figure(2)
surf(X,Y,IX)
xlabel('x')
ylabel('y')
zlabel('M')
hold on
plot(0,0)
figure(1)
surf(X,Y,DA)
hold on
plot(0,0)
clc
clear
LX=1;
LY=1;
M=10;
N=10;
DX=LX/M;
DY=LY/N;
X0=0;
Y0=0;
ii=-1;
for i=1:M+1;
ii=ii+1;
jj=-1;
for j=1:N+1;
jj=jj+1;
X(i,j)=ii*DX+X0;
Y(i,j)=jj*DY+Y0;
DA(i,j)=(DX)*(DY);
end
end
a1=size(X)
a2=size(Y)
xc=sum(sum(X))/(a1(1)*a1(2))
yc=sum(sum(Y))/(a2(1)*a2(2))
for i=1:M+1;
for j=1:N+1;
IX(i,j)=((Y(i,j)-yc)^2)*DA(i,j);
end
end
ix=(1/12)*(LX)*(LY)^3
A=sum(sum(DA))
IXX=sum(sum(IX))/(a1(1)*a1(2))
figure(2)
surf(X,Y,IX)
xlabel('x')
ylabel('y')
zlabel('M')
hold on
plot(0,0)
figure(1)
surf(X,Y,DA)
hold on
plot(0,0)
Unless otherwise noted, all content on this site is @Copyright by Ahmed Al Makky 2012-2013 - http://cfd2012.com