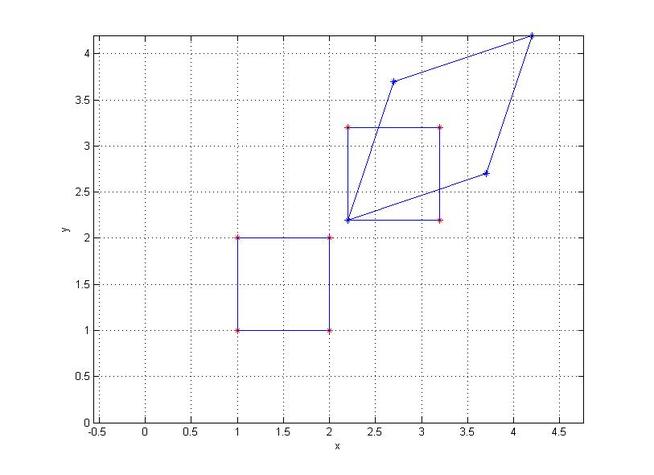
MATLAB Infinitesimal strain theory
This is a 2D code which I plane to extend to a three dimensional case.
clc
clear
X1=1;
Y1=1;
X2=2;
Y2=1;
X3=1;
Y3=2;
X4=2;
Y4=2;
dx=X2-X1;
dy=Y3-Y1;
plot(X1,Y1,'r*',X2,Y2,'r*',X3,Y3,'r*',X4,Y4,'r*')
hold on
plot(0,0)
V1X=[X1,X2]
V1Y=[Y1,Y2]
line(V1X,V1Y)
V2X=[X1,X3]
V2Y=[Y1,Y3]
line(V2X,V2Y)
V3X=[X3,X4]
V3Y=[Y3,Y4]
line(V3X,V3Y)
V4X=[X2,X4]
V4Y=[Y2,Y4]
line(V4X,V4Y)
grid on
xlabel('x')
ylabel('y')
X0=1.2;
Y0=1.2;
X11=1+X0;
Y11=1+Y0;
X22=2+X0;
Y22=1+Y0;
X33=1+X0;
Y33=2+Y0;
X44=2+X0;
Y44=2+Y0;
plot(X11,Y11,'r*',X22,Y22,'r*',X33,Y33,'r*',X44,Y44,'r*')
V11X=[X11,X22]
V11Y=[Y11,Y22]
line(V11X,V11Y)
V22X=[X11,X33]
V22Y=[Y11,Y33]
line(V22X,V22Y)
V33X=[X33,X44]
V33Y=[Y33,Y44]
line(V33X,V33Y)
V44X=[X22,X44]
V44Y=[Y22,Y44]
line(V44X,V44Y)
X111=1+X0;
Y111=1+Y0;
X222=2.5+X0;
Y222=1.5+Y0;
X333=1.5+X0;
Y333=2.5+Y0;
X444=3+X0;
Y444=3+Y0;
plot(X111,Y111,'b*',X222,Y222,'b*',X333,Y333,'b*',X444,Y444,'b*')
V111X=[X111,X222]
V111Y=[Y111,Y222]
line(V111X,V111Y)
V222X=[X111,X333]
V222Y=[Y111,Y333]
line(V222X,V222Y)
V333X=[X333,X444]
V333Y=[Y333,Y444]
line(V333X,V333Y)
V444X=[X222,X444]
V444Y=[Y222,Y444]
line(V444X,V444Y)
axis equal
UX0=X111-X1
UY0=Y222-Y2
UX=X222-X2
UY=Y333-Y3
DUxDXdx=X222-X22
DUyDXdx=Y222-Y11
aba=((dx+DUxDXdx)^2+(DUyDXdx)^2)^0.5
epx=(aba-dx)/dx
DUxDYdy=X333-X33
DUyDYdy=Y333-Y33
aca=((dy+DUyDYdy)^2+(DUxDYdy)^2)^0.5
epy=(aca-dy)/dy
alpha=DUyDXdx/(dx+DUxDXdx)
beta=DUxDYdy/(dy+DUyDYdy)
gamaxy=alpha+beta
gamayx=gamaxy
clear
X1=1;
Y1=1;
X2=2;
Y2=1;
X3=1;
Y3=2;
X4=2;
Y4=2;
dx=X2-X1;
dy=Y3-Y1;
plot(X1,Y1,'r*',X2,Y2,'r*',X3,Y3,'r*',X4,Y4,'r*')
hold on
plot(0,0)
V1X=[X1,X2]
V1Y=[Y1,Y2]
line(V1X,V1Y)
V2X=[X1,X3]
V2Y=[Y1,Y3]
line(V2X,V2Y)
V3X=[X3,X4]
V3Y=[Y3,Y4]
line(V3X,V3Y)
V4X=[X2,X4]
V4Y=[Y2,Y4]
line(V4X,V4Y)
grid on
xlabel('x')
ylabel('y')
X0=1.2;
Y0=1.2;
X11=1+X0;
Y11=1+Y0;
X22=2+X0;
Y22=1+Y0;
X33=1+X0;
Y33=2+Y0;
X44=2+X0;
Y44=2+Y0;
plot(X11,Y11,'r*',X22,Y22,'r*',X33,Y33,'r*',X44,Y44,'r*')
V11X=[X11,X22]
V11Y=[Y11,Y22]
line(V11X,V11Y)
V22X=[X11,X33]
V22Y=[Y11,Y33]
line(V22X,V22Y)
V33X=[X33,X44]
V33Y=[Y33,Y44]
line(V33X,V33Y)
V44X=[X22,X44]
V44Y=[Y22,Y44]
line(V44X,V44Y)
X111=1+X0;
Y111=1+Y0;
X222=2.5+X0;
Y222=1.5+Y0;
X333=1.5+X0;
Y333=2.5+Y0;
X444=3+X0;
Y444=3+Y0;
plot(X111,Y111,'b*',X222,Y222,'b*',X333,Y333,'b*',X444,Y444,'b*')
V111X=[X111,X222]
V111Y=[Y111,Y222]
line(V111X,V111Y)
V222X=[X111,X333]
V222Y=[Y111,Y333]
line(V222X,V222Y)
V333X=[X333,X444]
V333Y=[Y333,Y444]
line(V333X,V333Y)
V444X=[X222,X444]
V444Y=[Y222,Y444]
line(V444X,V444Y)
axis equal
UX0=X111-X1
UY0=Y222-Y2
UX=X222-X2
UY=Y333-Y3
DUxDXdx=X222-X22
DUyDXdx=Y222-Y11
aba=((dx+DUxDXdx)^2+(DUyDXdx)^2)^0.5
epx=(aba-dx)/dx
DUxDYdy=X333-X33
DUyDYdy=Y333-Y33
aca=((dy+DUyDYdy)^2+(DUxDYdy)^2)^0.5
epy=(aca-dy)/dy
alpha=DUyDXdx/(dx+DUxDXdx)
beta=DUxDYdy/(dy+DUyDYdy)
gamaxy=alpha+beta
gamayx=gamaxy
The following link provides the needed theory to understand the code
Unless otherwise noted, all content on this site is @Copyright by Ahmed Al Makky 2012-2013 - http://cfd2012.com