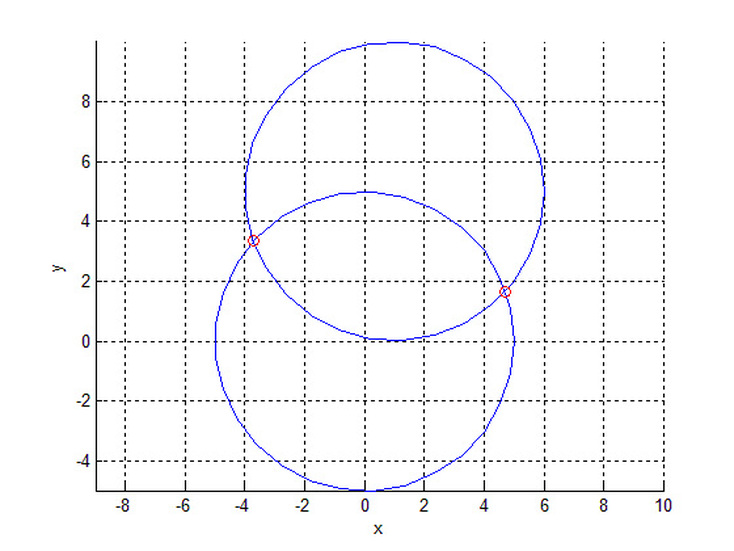
Finding Points of Intersection Between to Circules
clf
N=30; % circle resolution as the number of points
hold on
% draw 1st circle at (0,0) radius 5 and get X and Y data
H1=circle([0 0],5,N);
X1=get(H1,'XData');
Y1=get(H1,'YData');
% draw 2nd circle at (2,5) radius 3 and get X and Y data
H2=circle([1 5],5,N);
X2=get(H2,'XData');
Y2=get(H2,'YData');
% find intersection points
[x,y]=intersections(X1,Y1,X2,Y2,0);
% and plot them as red o's
plot(x,y,'ro')
grid on
xlabel('x')
ylabel('y')
hold off
axis equal
N=30; % circle resolution as the number of points
hold on
% draw 1st circle at (0,0) radius 5 and get X and Y data
H1=circle([0 0],5,N);
X1=get(H1,'XData');
Y1=get(H1,'YData');
% draw 2nd circle at (2,5) radius 3 and get X and Y data
H2=circle([1 5],5,N);
X2=get(H2,'XData');
Y2=get(H2,'YData');
% find intersection points
[x,y]=intersections(X1,Y1,X2,Y2,0);
% and plot them as red o's
plot(x,y,'ro')
grid on
xlabel('x')
ylabel('y')
hold off
axis equal
Note: The function code wasnt written by me downloaded from the net.
function [x0,y0,iout,jout] = intersections(x1,y1,x2,y2,robust)
%INTERSECTIONS Intersections of curves.
% Computes the (x,y) locations where two curves intersect. The curves
% can be broken with NaNs or have vertical segments.
%
% Example:
% [X0,Y0] = intersections(X1,Y1,X2,Y2,ROBUST);
%
% where X1 and Y1 are equal-length vectors of at least two points and
% represent curve 1. Similarly, X2 and Y2 represent curve 2.
% X0 and Y0 are column vectors containing the points at which the two
% curves intersect.
%
% ROBUST (optional) set to 1 or true means to use a slight variation of the
% algorithm that might return duplicates of some intersection points, and
% then remove those duplicates. The default is true, but since the
% algorithm is slightly slower you can set it to false if you know that
% your curves don't intersect at any segment boundaries. Also, the robust
% version properly handles parallel and overlapping segments.
%
% The algorithm can return two additional vectors that indicate which
% segment pairs contain intersections and where they are:
%
% [X0,Y0,I,J] = intersections(X1,Y1,X2,Y2,ROBUST);
%
% For each element of the vector I, I(k) = (segment number of (X1,Y1)) +
% (how far along this segment the intersection is). For example, if I(k) =
% 45.25 then the intersection lies a quarter of the way between the line
% segment connecting (X1(45),Y1(45)) and (X1(46),Y1(46)). Similarly for
% the vector J and the segments in (X2,Y2).
%
% You can also get intersections of a curve with itself. Simply pass in
% only one curve, i.e.,
%
% [X0,Y0] = intersections(X1,Y1,ROBUST);
%
% where, as before, ROBUST is optional.
% Version: 1.12, 27 January 2010
% Author: Douglas M. Schwarz
% Email: dmschwarz=ieee*org, dmschwarz=urgrad*rochester*edu
% Real_email = regexprep(Email,{'=','*'},{'@','.'})
% Theory of operation:
%
% Given two line segments, L1 and L2,
%
% L1 endpoints: (x1(1),y1(1)) and (x1(2),y1(2))
% L2 endpoints: (x2(1),y2(1)) and (x2(2),y2(2))
%
% we can write four equations with four unknowns and then solve them. The
% four unknowns are t1, t2, x0 and y0, where (x0,y0) is the intersection of
% L1 and L2, t1 is the distance from the starting point of L1 to the
% intersection relative to the length of L1 and t2 is the distance from the
% starting point of L2 to the intersection relative to the length of L2.
%
% So, the four equations are
%
% (x1(2) - x1(1))*t1 = x0 - x1(1)
% (x2(2) - x2(1))*t2 = x0 - x2(1)
% (y1(2) - y1(1))*t1 = y0 - y1(1)
% (y2(2) - y2(1))*t2 = y0 - y2(1)
%
% Rearranging and writing in matrix form,
%
% [x1(2)-x1(1) 0 -1 0; [t1; [-x1(1);
% 0 x2(2)-x2(1) -1 0; * t2; = -x2(1);
% y1(2)-y1(1) 0 0 -1; x0; -y1(1);
% 0 y2(2)-y2(1) 0 -1] y0] -y2(1)]
%
% Let's call that A*T = B. We can solve for T with T = A\B.
%
% Once we have our solution we just have to look at t1 and t2 to determine
% whether L1 and L2 intersect. If 0 <= t1 < 1 and 0 <= t2 < 1 then the two
% line segments cross and we can include (x0,y0) in the output.
%
% In principle, we have to perform this computation on every pair of line
% segments in the input data. This can be quite a large number of pairs so
% we will reduce it by doing a simple preliminary check to eliminate line
% segment pairs that could not possibly cross. The check is to look at the
% smallest enclosing rectangles (with sides parallel to the axes) for each
% line segment pair and see if they overlap. If they do then we have to
% compute t1 and t2 (via the A\B computation) to see if the line segments
% cross, but if they don't then the line segments cannot cross. In a
% typical application, this technique will eliminate most of the potential
% line segment pairs.
% Input checks.
error(nargchk(2,5,nargin))
% Adjustments when fewer than five arguments are supplied.
switch nargin
case 2
robust = true;
x2 = x1;
y2 = y1;
self_intersect = true;
case 3
robust = x2;
x2 = x1;
y2 = y1;
self_intersect = true;
case 4
robust = true;
self_intersect = false;
case 5
self_intersect = false;
end
% x1 and y1 must be vectors with same number of points (at least 2).
if sum(size(x1) > 1) ~= 1 || sum(size(y1) > 1) ~= 1 || ...
length(x1) ~= length(y1)
error('X1 and Y1 must be equal-length vectors of at least 2 points.')
end
% x2 and y2 must be vectors with same number of points (at least 2).
if sum(size(x2) > 1) ~= 1 || sum(size(y2) > 1) ~= 1 || ...
length(x2) ~= length(y2)
error('X2 and Y2 must be equal-length vectors of at least 2 points.')
end
% Force all inputs to be column vectors.
x1 = x1(:);
y1 = y1(:);
x2 = x2(:);
y2 = y2(:);
% Compute number of line segments in each curve and some differences we'll
% need later.
n1 = length(x1) - 1;
n2 = length(x2) - 1;
xy1 = [x1 y1];
xy2 = [x2 y2];
dxy1 = diff(xy1);
dxy2 = diff(xy2);
% Determine the combinations of i and j where the rectangle enclosing the
% i'th line segment of curve 1 overlaps with the rectangle enclosing the
% j'th line segment of curve 2.
[i,j] = find(repmat(min(x1(1:end-1),x1(2:end)),1,n2) <= ...
repmat(max(x2(1:end-1),x2(2:end)).',n1,1) & ...
repmat(max(x1(1:end-1),x1(2:end)),1,n2) >= ...
repmat(min(x2(1:end-1),x2(2:end)).',n1,1) & ...
repmat(min(y1(1:end-1),y1(2:end)),1,n2) <= ...
repmat(max(y2(1:end-1),y2(2:end)).',n1,1) & ...
repmat(max(y1(1:end-1),y1(2:end)),1,n2) >= ...
repmat(min(y2(1:end-1),y2(2:end)).',n1,1));
% Force i and j to be column vectors, even when their length is zero, i.e.,
% we want them to be 0-by-1 instead of 0-by-0.
i = reshape(i,[],1);
j = reshape(j,[],1);
% Find segments pairs which have at least one vertex = NaN and remove them.
% This line is a fast way of finding such segment pairs. We take
% advantage of the fact that NaNs propagate through calculations, in
% particular subtraction (in the calculation of dxy1 and dxy2, which we
% need anyway) and addition.
% At the same time we can remove redundant combinations of i and j in the
% case of finding intersections of a line with itself.
if self_intersect
remove = isnan(sum(dxy1(i,:) + dxy2(j,:),2)) | j <= i + 1;
else
remove = isnan(sum(dxy1(i,:) + dxy2(j,:),2));
end
i(remove) = [];
j(remove) = [];
% Initialize matrices. We'll put the T's and B's in matrices and use them
% one column at a time. AA is a 3-D extension of A where we'll use one
% plane at a time.
n = length(i);
T = zeros(4,n);
AA = zeros(4,4,n);
AA([1 2],3,:) = -1;
AA([3 4],4,:) = -1;
AA([1 3],1,:) = dxy1(i,:).';
AA([2 4],2,:) = dxy2(j,:).';
B = -[x1(i) x2(j) y1(i) y2(j)].';
% Loop through possibilities. Trap singularity warning and then use
% lastwarn to see if that plane of AA is near singular. Process any such
% segment pairs to determine if they are colinear (overlap) or merely
% parallel. That test consists of checking to see if one of the endpoints
% of the curve 2 segment lies on the curve 1 segment. This is done by
% checking the cross product
%
% (x1(2),y1(2)) - (x1(1),y1(1)) x (x2(2),y2(2)) - (x1(1),y1(1)).
%
% If this is close to zero then the segments overlap.
% If the robust option is false then we assume no two segment pairs are
% parallel and just go ahead and do the computation. If A is ever singular
% a warning will appear. This is faster and obviously you should use it
% only when you know you will never have overlapping or parallel segment
% pairs.
if robust
overlap = false(n,1);
warning_state = warning('off','MATLAB:singularMatrix');
% Use try-catch to guarantee original warning state is restored.
try
lastwarn('')
for k = 1:n
T(:,k) = AA(:,:,k)\B(:,k);
[unused,last_warn] = lastwarn;
lastwarn('')
if strcmp(last_warn,'MATLAB:singularMatrix')
% Force in_range(k) to be false.
T(1,k) = NaN;
% Determine if these segments overlap or are just parallel.
overlap(k) = rcond([dxy1(i(k),:);xy2(j(k),:) - xy1(i(k),:)]) < eps;
end
end
warning(warning_state)
catch err
warning(warning_state)
rethrow(err)
end
% Find where t1 and t2 are between 0 and 1 and return the corresponding
% x0 and y0 values.
in_range = (T(1,:) >= 0 & T(2,:) >= 0 & T(1,:) <= 1 & T(2,:) <= 1).';
% For overlapping segment pairs the algorithm will return an
% intersection point that is at the center of the overlapping region.
if any(overlap)
ia = i(overlap);
ja = j(overlap);
% set x0 and y0 to middle of overlapping region.
T(3,overlap) = (max(min(x1(ia),x1(ia+1)),min(x2(ja),x2(ja+1))) + ...
min(max(x1(ia),x1(ia+1)),max(x2(ja),x2(ja+1)))).'/2;
T(4,overlap) = (max(min(y1(ia),y1(ia+1)),min(y2(ja),y2(ja+1))) + ...
min(max(y1(ia),y1(ia+1)),max(y2(ja),y2(ja+1)))).'/2;
selected = in_range | overlap;
else
selected = in_range;
end
xy0 = T(3:4,selected).';
% Remove duplicate intersection points.
[xy0,index] = unique(xy0,'rows');
x0 = xy0(:,1);
y0 = xy0(:,2);
% Compute how far along each line segment the intersections are.
if nargout > 2
sel_index = find(selected);
sel = sel_index(index);
iout = i(sel) + T(1,sel).';
jout = j(sel) + T(2,sel).';
end
else % non-robust option
for k = 1:n
[L,U] = lu(AA(:,:,k));
T(:,k) = U\(L\B(:,k));
end
% Find where t1 and t2 are between 0 and 1 and return the corresponding
% x0 and y0 values.
in_range = (T(1,:) >= 0 & T(2,:) >= 0 & T(1,:) < 1 & T(2,:) < 1).';
x0 = T(3,in_range).';
y0 = T(4,in_range).';
% Compute how far along each line segment the intersections are.
if nargout > 2
iout = i(in_range) + T(1,in_range).';
jout = j(in_range) + T(2,in_range).';
end
end
% Plot the results (useful for debugging).
% plot(x1,y1,x2,y2,x0,y0,'ok');
%INTERSECTIONS Intersections of curves.
% Computes the (x,y) locations where two curves intersect. The curves
% can be broken with NaNs or have vertical segments.
%
% Example:
% [X0,Y0] = intersections(X1,Y1,X2,Y2,ROBUST);
%
% where X1 and Y1 are equal-length vectors of at least two points and
% represent curve 1. Similarly, X2 and Y2 represent curve 2.
% X0 and Y0 are column vectors containing the points at which the two
% curves intersect.
%
% ROBUST (optional) set to 1 or true means to use a slight variation of the
% algorithm that might return duplicates of some intersection points, and
% then remove those duplicates. The default is true, but since the
% algorithm is slightly slower you can set it to false if you know that
% your curves don't intersect at any segment boundaries. Also, the robust
% version properly handles parallel and overlapping segments.
%
% The algorithm can return two additional vectors that indicate which
% segment pairs contain intersections and where they are:
%
% [X0,Y0,I,J] = intersections(X1,Y1,X2,Y2,ROBUST);
%
% For each element of the vector I, I(k) = (segment number of (X1,Y1)) +
% (how far along this segment the intersection is). For example, if I(k) =
% 45.25 then the intersection lies a quarter of the way between the line
% segment connecting (X1(45),Y1(45)) and (X1(46),Y1(46)). Similarly for
% the vector J and the segments in (X2,Y2).
%
% You can also get intersections of a curve with itself. Simply pass in
% only one curve, i.e.,
%
% [X0,Y0] = intersections(X1,Y1,ROBUST);
%
% where, as before, ROBUST is optional.
% Version: 1.12, 27 January 2010
% Author: Douglas M. Schwarz
% Email: dmschwarz=ieee*org, dmschwarz=urgrad*rochester*edu
% Real_email = regexprep(Email,{'=','*'},{'@','.'})
% Theory of operation:
%
% Given two line segments, L1 and L2,
%
% L1 endpoints: (x1(1),y1(1)) and (x1(2),y1(2))
% L2 endpoints: (x2(1),y2(1)) and (x2(2),y2(2))
%
% we can write four equations with four unknowns and then solve them. The
% four unknowns are t1, t2, x0 and y0, where (x0,y0) is the intersection of
% L1 and L2, t1 is the distance from the starting point of L1 to the
% intersection relative to the length of L1 and t2 is the distance from the
% starting point of L2 to the intersection relative to the length of L2.
%
% So, the four equations are
%
% (x1(2) - x1(1))*t1 = x0 - x1(1)
% (x2(2) - x2(1))*t2 = x0 - x2(1)
% (y1(2) - y1(1))*t1 = y0 - y1(1)
% (y2(2) - y2(1))*t2 = y0 - y2(1)
%
% Rearranging and writing in matrix form,
%
% [x1(2)-x1(1) 0 -1 0; [t1; [-x1(1);
% 0 x2(2)-x2(1) -1 0; * t2; = -x2(1);
% y1(2)-y1(1) 0 0 -1; x0; -y1(1);
% 0 y2(2)-y2(1) 0 -1] y0] -y2(1)]
%
% Let's call that A*T = B. We can solve for T with T = A\B.
%
% Once we have our solution we just have to look at t1 and t2 to determine
% whether L1 and L2 intersect. If 0 <= t1 < 1 and 0 <= t2 < 1 then the two
% line segments cross and we can include (x0,y0) in the output.
%
% In principle, we have to perform this computation on every pair of line
% segments in the input data. This can be quite a large number of pairs so
% we will reduce it by doing a simple preliminary check to eliminate line
% segment pairs that could not possibly cross. The check is to look at the
% smallest enclosing rectangles (with sides parallel to the axes) for each
% line segment pair and see if they overlap. If they do then we have to
% compute t1 and t2 (via the A\B computation) to see if the line segments
% cross, but if they don't then the line segments cannot cross. In a
% typical application, this technique will eliminate most of the potential
% line segment pairs.
% Input checks.
error(nargchk(2,5,nargin))
% Adjustments when fewer than five arguments are supplied.
switch nargin
case 2
robust = true;
x2 = x1;
y2 = y1;
self_intersect = true;
case 3
robust = x2;
x2 = x1;
y2 = y1;
self_intersect = true;
case 4
robust = true;
self_intersect = false;
case 5
self_intersect = false;
end
% x1 and y1 must be vectors with same number of points (at least 2).
if sum(size(x1) > 1) ~= 1 || sum(size(y1) > 1) ~= 1 || ...
length(x1) ~= length(y1)
error('X1 and Y1 must be equal-length vectors of at least 2 points.')
end
% x2 and y2 must be vectors with same number of points (at least 2).
if sum(size(x2) > 1) ~= 1 || sum(size(y2) > 1) ~= 1 || ...
length(x2) ~= length(y2)
error('X2 and Y2 must be equal-length vectors of at least 2 points.')
end
% Force all inputs to be column vectors.
x1 = x1(:);
y1 = y1(:);
x2 = x2(:);
y2 = y2(:);
% Compute number of line segments in each curve and some differences we'll
% need later.
n1 = length(x1) - 1;
n2 = length(x2) - 1;
xy1 = [x1 y1];
xy2 = [x2 y2];
dxy1 = diff(xy1);
dxy2 = diff(xy2);
% Determine the combinations of i and j where the rectangle enclosing the
% i'th line segment of curve 1 overlaps with the rectangle enclosing the
% j'th line segment of curve 2.
[i,j] = find(repmat(min(x1(1:end-1),x1(2:end)),1,n2) <= ...
repmat(max(x2(1:end-1),x2(2:end)).',n1,1) & ...
repmat(max(x1(1:end-1),x1(2:end)),1,n2) >= ...
repmat(min(x2(1:end-1),x2(2:end)).',n1,1) & ...
repmat(min(y1(1:end-1),y1(2:end)),1,n2) <= ...
repmat(max(y2(1:end-1),y2(2:end)).',n1,1) & ...
repmat(max(y1(1:end-1),y1(2:end)),1,n2) >= ...
repmat(min(y2(1:end-1),y2(2:end)).',n1,1));
% Force i and j to be column vectors, even when their length is zero, i.e.,
% we want them to be 0-by-1 instead of 0-by-0.
i = reshape(i,[],1);
j = reshape(j,[],1);
% Find segments pairs which have at least one vertex = NaN and remove them.
% This line is a fast way of finding such segment pairs. We take
% advantage of the fact that NaNs propagate through calculations, in
% particular subtraction (in the calculation of dxy1 and dxy2, which we
% need anyway) and addition.
% At the same time we can remove redundant combinations of i and j in the
% case of finding intersections of a line with itself.
if self_intersect
remove = isnan(sum(dxy1(i,:) + dxy2(j,:),2)) | j <= i + 1;
else
remove = isnan(sum(dxy1(i,:) + dxy2(j,:),2));
end
i(remove) = [];
j(remove) = [];
% Initialize matrices. We'll put the T's and B's in matrices and use them
% one column at a time. AA is a 3-D extension of A where we'll use one
% plane at a time.
n = length(i);
T = zeros(4,n);
AA = zeros(4,4,n);
AA([1 2],3,:) = -1;
AA([3 4],4,:) = -1;
AA([1 3],1,:) = dxy1(i,:).';
AA([2 4],2,:) = dxy2(j,:).';
B = -[x1(i) x2(j) y1(i) y2(j)].';
% Loop through possibilities. Trap singularity warning and then use
% lastwarn to see if that plane of AA is near singular. Process any such
% segment pairs to determine if they are colinear (overlap) or merely
% parallel. That test consists of checking to see if one of the endpoints
% of the curve 2 segment lies on the curve 1 segment. This is done by
% checking the cross product
%
% (x1(2),y1(2)) - (x1(1),y1(1)) x (x2(2),y2(2)) - (x1(1),y1(1)).
%
% If this is close to zero then the segments overlap.
% If the robust option is false then we assume no two segment pairs are
% parallel and just go ahead and do the computation. If A is ever singular
% a warning will appear. This is faster and obviously you should use it
% only when you know you will never have overlapping or parallel segment
% pairs.
if robust
overlap = false(n,1);
warning_state = warning('off','MATLAB:singularMatrix');
% Use try-catch to guarantee original warning state is restored.
try
lastwarn('')
for k = 1:n
T(:,k) = AA(:,:,k)\B(:,k);
[unused,last_warn] = lastwarn;
lastwarn('')
if strcmp(last_warn,'MATLAB:singularMatrix')
% Force in_range(k) to be false.
T(1,k) = NaN;
% Determine if these segments overlap or are just parallel.
overlap(k) = rcond([dxy1(i(k),:);xy2(j(k),:) - xy1(i(k),:)]) < eps;
end
end
warning(warning_state)
catch err
warning(warning_state)
rethrow(err)
end
% Find where t1 and t2 are between 0 and 1 and return the corresponding
% x0 and y0 values.
in_range = (T(1,:) >= 0 & T(2,:) >= 0 & T(1,:) <= 1 & T(2,:) <= 1).';
% For overlapping segment pairs the algorithm will return an
% intersection point that is at the center of the overlapping region.
if any(overlap)
ia = i(overlap);
ja = j(overlap);
% set x0 and y0 to middle of overlapping region.
T(3,overlap) = (max(min(x1(ia),x1(ia+1)),min(x2(ja),x2(ja+1))) + ...
min(max(x1(ia),x1(ia+1)),max(x2(ja),x2(ja+1)))).'/2;
T(4,overlap) = (max(min(y1(ia),y1(ia+1)),min(y2(ja),y2(ja+1))) + ...
min(max(y1(ia),y1(ia+1)),max(y2(ja),y2(ja+1)))).'/2;
selected = in_range | overlap;
else
selected = in_range;
end
xy0 = T(3:4,selected).';
% Remove duplicate intersection points.
[xy0,index] = unique(xy0,'rows');
x0 = xy0(:,1);
y0 = xy0(:,2);
% Compute how far along each line segment the intersections are.
if nargout > 2
sel_index = find(selected);
sel = sel_index(index);
iout = i(sel) + T(1,sel).';
jout = j(sel) + T(2,sel).';
end
else % non-robust option
for k = 1:n
[L,U] = lu(AA(:,:,k));
T(:,k) = U\(L\B(:,k));
end
% Find where t1 and t2 are between 0 and 1 and return the corresponding
% x0 and y0 values.
in_range = (T(1,:) >= 0 & T(2,:) >= 0 & T(1,:) < 1 & T(2,:) < 1).';
x0 = T(3,in_range).';
y0 = T(4,in_range).';
% Compute how far along each line segment the intersections are.
if nargout > 2
iout = i(in_range) + T(1,in_range).';
jout = j(in_range) + T(2,in_range).';
end
end
% Plot the results (useful for debugging).
% plot(x1,y1,x2,y2,x0,y0,'ok');
Unless otherwise noted, all content on this site is @Copyright by Ahmed Al Makky 2012-2013 - http://cfd2012.com